Fähigkeiten
Für das Abitur sollten Sie folgende können:
- Zu zwei gegebenen Richtungsvektoren einen Normalenvektor ermitteln.
- Aus drei Punkten eine Ebenengleichung ermitteln, egal in welcher Form.
- Die Parameterform in eine Koordinatenform oder in eine Normalenform umwandeln.
- Die Hesse'sche Normalenform aufstellen.
Wir werden nun ohne weitere "Theorie" diese Fähigkeiten anhand verschiedener Aufgaben üben.
Aufgabe 1
Liegen die Punkte A(1|1|1), B(0|2|0), C(1|2|-2) und D(4|5|-17) in einer Ebene?
Lösung
Wir bestimmen zunächst die Richtungsvektoren
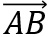und 
.
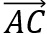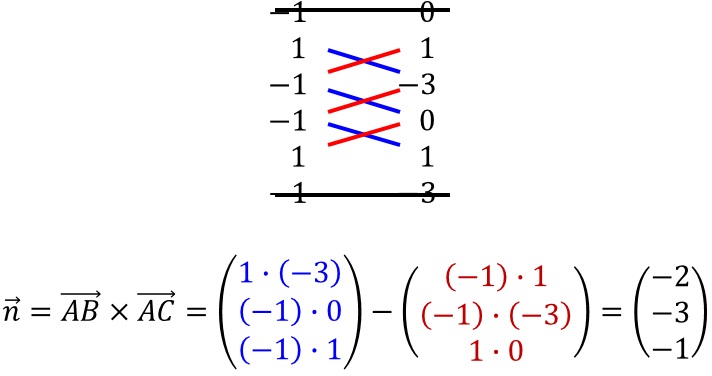
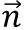noch mit -1.
Dadurch werden wir die lästigen Vorzeichen los und das neue
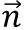steht immer noch senkrecht zu den Richtungsvektoren, da sich ja nun lediglich die Richtung des alten
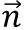umgedreht hat.Wir haben also
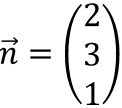als
Normalenvektor.Daraus ergibt sich die noch unvollständige Koordinatenform:
E: 2x1+3x2+x3=d
Durch Einsetzen von A(1|1|1) erhalten wir d=6.Somit haben wir E: 2x1+3x2+x3=6.
Nun setzen wir der Reihe nach die restlichen Punkte B(0|2|0), C(1|2|-2) und D(4|5|-17) ein und prüfen, ob die Gleichung jeweils erfüllt wird.
B(0|2|0): 2·0+3·2+0=6 → OK!
C(1|2|-2): 2·1+3·2+(-2)=6 → OK!
D(4|5|-17): 2·4+3·5+(-17)=6 → OK!
Ergebnis: Alle Punkte liegen in derselben Ebene!
Aufgabe 2
Wandle die Parameterform
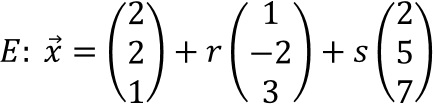zunächst
in die Normalenform und anschließend in die Koordinatenform um.Liegen die Punkte P(-1|-10|-10) und Q(-1|29|6) in E?
Lösung
Wir bilden aus den beiden Spannvektoren (auch Richtungsvektoren genannt) mit dem Vektorprodukt zuerst einen Normalenvektor.
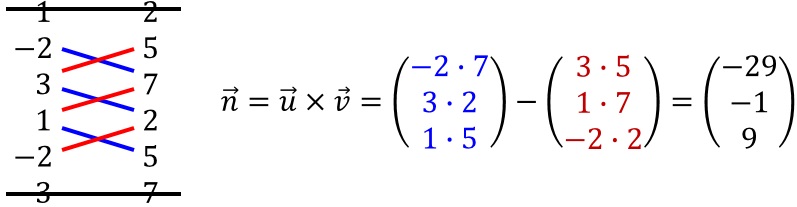
Wir erhalten
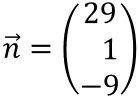als neuen Normalenvektor.Mit dem Stützvektor
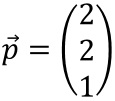aus der Parameterform ergibt sich daraus die Normalenform:
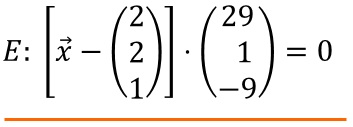
Die Koordinatenform kann man auf zwei Wegen erhalten.
Methode 1: Ausmultiplizieren der Normalenform
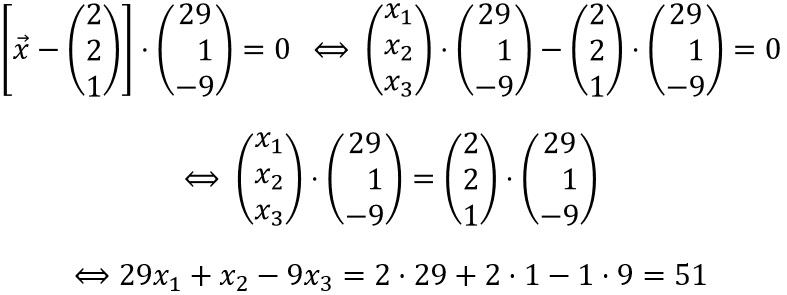
Methode 2:
Der Normalenvektor liefert folgenden Ansatz 29x1+x2-9x3=d.
Das noch unbekannte d bestimmt man, in dem man einen Punkt einsetzt, der in der Ebene liegt, z.B. den Punkt, der durch den Stützvektor beschrieben wird.
Einsetzen des Stützvektors liefert 29·2+2-9·1=51=d.
Diese Methode erscheint uns am einfachsten!
Ergebnis: Die Koordinatenform lautet E: 29x1+x2-9x3=51.
Aufgabe 3
Die Punkte A(0|0|0) und C(4|8|0) sind Eckpunkte eines Quaders mit der Höhe h=5 LE2.
- Bestimme die restlichen Eckpunkte.
- Ermittle eine Parameterform der Ebene, in der die Punkte A, C und G liegen.
Ermitteln Sie weiterhin eine Normalenform, die Hesse‘sche Normalenform und die Koordinatenform. - Zeichne den Quader in ein Koordinatensystem und berechne dessen Volumen.
Lösungen für 1. und 3.
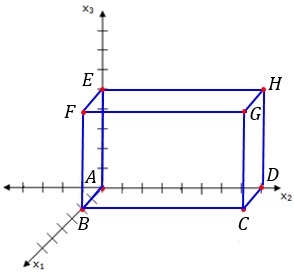
Die restlichen Eckpunkte sind B(4|0|0), D(0|8|0), E(0|0|5), F(4|0|5), G(4|8|5) und H(0|8|5). An den Koordinaten kann man die Längen des Quaders ablesen:
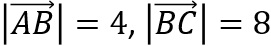und h=5 (war vorgegeben).Damit ergibt sich das Volumen des Quaders mit V=4·8·5=160 LE3.
Lösung für 2.
Parameterform für E:
Aus den Punkten A, C und G ergeben sich die Richtungsvektoren
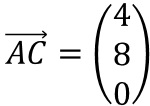und
.
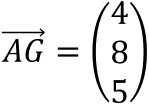Wenn wir den Ortsvektor zum Punkt A als Stützvektor verwenden, erhalten wir sofort eine Parameterform für E.
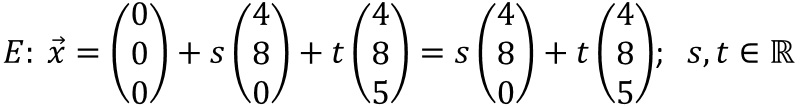
Normalenform für E:
Aus den Richtungsvektoren
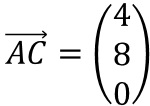und 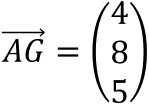ergibt
sich mit dem Vektorprodukt zunächst ein Normalenvektor.
.
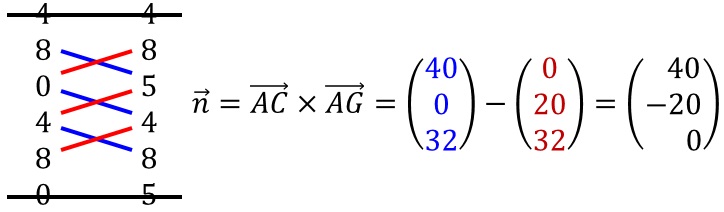
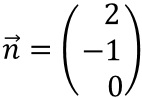Mit dem Nullvektor als Stützvektor ergibt sich daraus die Normalenform für E: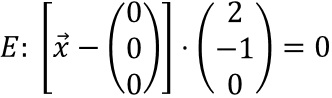
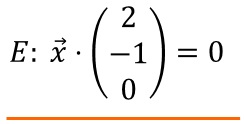
Koordinatenform für E:
Mit dem Normalenvektor
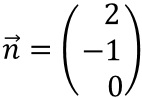ergibt sich auch gleich die Koordinatenform mit
E: 2x1-x2+0x3=d.
Da der Ursprung in E liegt erhalten wir durch Einsetzen den Wert d=0 und damit die komplette Koordinatenform:E: 2x1-x2=0
Hesse‘sche Normalenform für E:
Mit
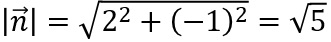ergibt
sich aus der Koordinatenform (siehe oben) nach Division durch die Länge des Normalenvektors die
Koordinatenform in Parameterform umwandeln
Fragestellungen dieser Art kommen im Abi eher selten vor. Dennoch, sozusagen der Vollständigkeit wegen, möchte ich Ihnen an dieser Stelle nochmal ins Gedächtnis rufen, wie man die Koordinatenform einer Ebene zurückwandelt in eine Parameterform.
Vorgegeben sei irgendeine Ebene in Koordinatenform E: ax1+bx2+cx3=d.
Gesucht ist eine Parameterform von E.
Vorgehensweise
Finde drei Punkte A, B und C, die alle in E aber nicht auf einer Geraden liegen. Der Einfachheit halber verwendet man hierfür die Spurpunkte von E.
Zur Erinnerung: Die Spurpunkte sind die Schnittpunkte der Ebene mit den Koordinatenachsen. Man bekommt sie, indem man in der Koordinatengleichung jeweils zwei Koordinaten 0 setzt und nach der dritten Koordinate auflöst. Wir werden das gleich im Rechenbeispiel nochmal verdeutlichen.
Um die Parameterform zu erhalten können Sie dann den Ortsvektor von A als Stützvektor verwenden und beispielsweise die Verbindungsvektoren von A nach B und von A nach C als Richtungsvektoren. Formal:
In
ist dann 
und 
.Rechenbeispiel
Wandle E: 2x1+8x2+4x3=16 um in eine Parameterform.
Lösung
Die Spurpunkte von E sind A(8|0|0), B(0|2|0) und C(0|0|4).
Damit ist
ein Stützvektor und 
und 
können wir als Richtungsvektoren (=Spannvektoren) verwenden. Damit haben wir eine Parameterform:
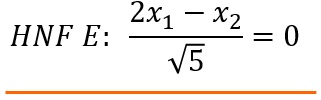
| Downloads |
PowerPoint